Weight Initialization

A note to self

When designing a deep learning architecture, the statistical properties of the propagating is an important consideration to take note of.

With proper initialization, one can ensure that variance is conserved in the forward / backward pass (you gotta choose one cuz they propagate differently) when the network was first initialized. The concept of Equalized Learning Rate preserves the variance in runtime and hence makes weight initialization not as important.

https://towardsdatascience.com/weight-initialization-in-neural-networks-a-journey-from-the-basics-to-kaiming-954fb9b47c79

Xavier Initialization

http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf

Used for tanh

https://cs230.stanford.edu/section/4/

$$W_{i,j}^{[l]}=\mathcal{N}(0,\frac{1}{n^{[l-1]}})$$

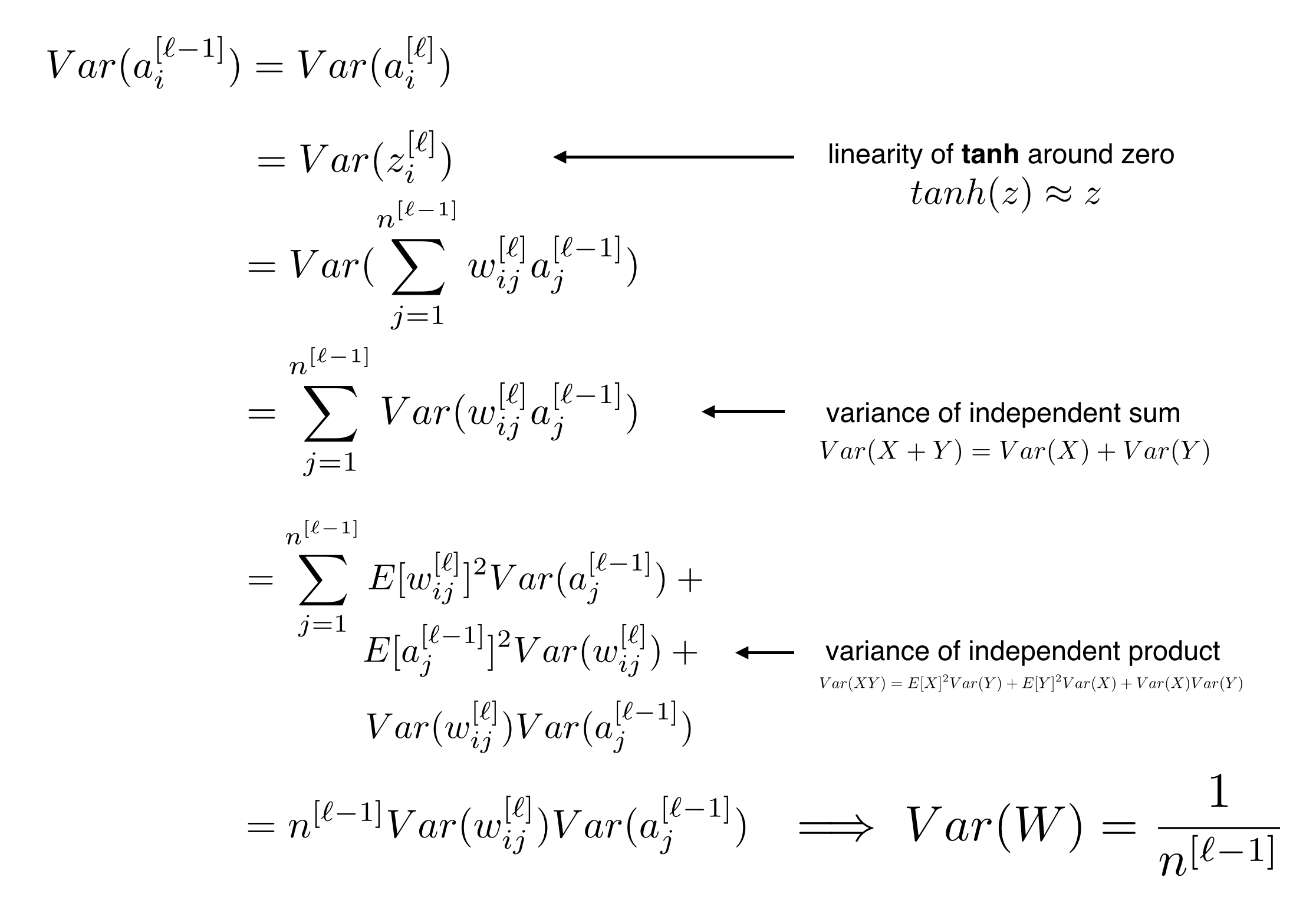
https://towardsdatascience.com/weight-initialization-in-neural-networks-a-journey-from-the-basics-to-kaiming-954fb9b47c79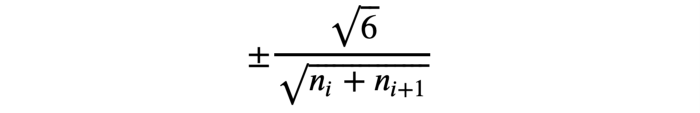

I guess both preserves the variance (you have xavier_uniform_ and xavier_normal_ in Pytorch)

Kaiming He Initialization

Since ReLU does not have mean zero, we need some adjustments

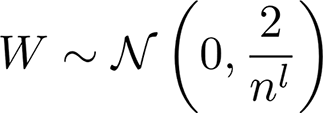
Proof: https://medium.com/@shoray.goel/kaiming-he-initialization-a8d9ed0b5899

Does Gain matter?

https://jamesmccaffrey.wordpress.com/2020/11/20/the-gain-parameter-for-the-pytorch-xavier_uniform_-and-xavier_normal_-initialization-functions/

Bias Term

https://stackoverflow.com/questions/44883861/initial-bias-values-for-a-neural-network